The Lunar Tidal Model - Part 1

AIM: To link the inter-decadal to centennial lunar tidal cycles to sub-decadal tidal processes that play a role in initiating El Nino events.

SUMMARY

El Ninos are preceded by westerly wind-bursts in the equatorial western Pacific Ocean that decreases the strength of the easterly equatorial trade-winds. These westerly wind-bursts are produced by twin low-pressure cells that straddle the Earth's equator in the western Pacific Ocean. These low-pressure cells are part of the westerly moving equatorial Rossby waves that are generated in near the location of the active phase of a Madden Julian Oscillation (MJO). 

Observational evidence indicates that El Ninos events must be initiated by a physical phenomenon that occurs at times when the Moon is closest to the Earth (i.e. Perigee) and when the lunar-induced acceleration of the Earth's rotation changes sign (i.e. at the times of lunar crossings and lunar standstills).

The lunar-induced acceleration of the Earth changes sign when the lunar-induced atmospheric /oceanic tidal height at the Earth's equator reaches an ebb, either at a tidal minimum (i.e. at a lunar standstill) or at a tidal maximum (i.e. at a lunar equatorial crossing).

This implies that equatorial Rossby waves in the active phase of an MJO are likely to be generated when the lunar-induced atmospheric/oceanic tidal height at the Earth's equator reaches an ebb, either at a tidal minimum (i.e. at a lunar standstill) or at a tidal maximum (i.e. at a lunar equatorial crossing).    
    
A. Inter-Decadal to Centennial Timescales  

Wilson and Sidorenkov 2018 (hereafter paper I) show that the epochs when the lunar line-of-apse points directly towards/away from the Sun, at times that are closely aligned with the Equinoxes and Solstices (i.e. seasonal boundaries), exhibit distinct periodicities at 28.75, 31.00, 88.50, 148.25, and 208.00 years. In addition, this paper notes that these specific periodicities only arise when the close lunar alignments are viewed in a frame of reference that is fixed with respect to the perihelion of the Earth’s orbit.

The full significance of this 208.0-year repetition pattern only becomes apparent when the periodicities in these seasonal luni-solar alignments (ϕ) are compared with the periodicities observed in the spectra for two proxy time series. The first series is the amplitude spectrum of the maximum daytime temperatures (Tm) on the Southern Colorado Plateau for the period from 266 BC to 1997 AD (Ron et al. 2012, Salzer and Kipfmueller 2005). The second is the Fourier spectrum of the solar modulation potential (ϕm) over the last 9400 years (Abreu et al. 2012, McCracken et al. 2013). Note that ϕm is considered to be a proxy index for the changing level of solar activity with time. When a comparison is made between these three spectra in paper I, it shows that of the nine most prominent peaks in the spectrum of ϕ, eight have matching peaks in the spectrum of ϕm, and seven have matching peaks in the spectrum of Tm. Hence, the paper concludes that all three of these phenomena must be related to one another.

Bottom line: The close matches between the periods of the prominent peaks that are seen in spectra of ϕ [as opposed to ϕm] and Tm in paper I, indicate that a factor that is associated with the epochs when the lunar line-of-apse points directly towards/away from the Sun, at times that are close to seasonal boundaries, must have an influence on the Earth’s world mean temperature on inter-decadal to centennial timescales.

This prompts the question: Is there some specific lunar tidal phenomenon that is a short term counterpart to the seasonal luni-solar alignments that operate on centennial timescales?

Wilson and Sidorenkov 2019 (hereafter paper II) shows that the Perigean New/Full moon tidal cycles that exhibit the least drift (i.e. the best temporal alignment) with respect to the seasons are the closest short-term counterpart to the centennial-scale luni-solar alignments that are discussed in Paper I. The caveat being that both sets of alignments have to be observed in a frame of reference that was fixed with respect to the Perihelion of the Earth’s orbit.

The figure above shows all the pseudo-cycles that are generated by the interaction between the 2.25, 4.5, 6.75, and 9.00-year [lunar] cycles with the 31.0-year [Perigean New/Full moon lunar] cycle. Firstly, the 2.25-year cycle generates the 28.75, 59.75, and 90.75-year pseudo-cycles. Secondly, the 4.50-year cycle generates the 88.5, 119.5, 150.5, and 181.5-year pseudo-cycles. Thirdly, the 6.75-year cycle generates the 148.25, 179.25, and 210.25-year pseudo-cycles, and finally, the 9.00-year cycle generates the 115, 146, 177, 208, and 239-year pseudo-cycles.

In order for a Perigean New/Full moon cycle to be aligned with the seasons, it would have to lie on or close to the red horizontal line in this figure [Note that the lunar cycles that are on this line are fixed in a reference frame that is precessing at the same rate as the rotation axis of the Earth]. The above figure shows that the cycles that best fit this description are all simple whole multiples of the sum of the 28.75-year and 31.00-year lunar cycles i.e. they are those with periods of 59.75, 119.5, 179.25 and 239.0 years. This means that, on inter-decadal to centennial time scales, the Perigean New/Full moon events that are best aligned with the seasonal calendar reoccur at intervals of 59.75 years, which is very close to 60 years.

Alternatively, if Perigean New/Full moon cycle is viewed in a frame of reference that aligns with the Perihelion of the Earth’s orbit, they would lie along the red dashed line in figure 4. The cycles that best fit this description in this figure are the 59.75, 88.5, 148.25 and 208.0-year cycles [N.B. the 119.5-year cycle is just a multiple of the 59.75-year cycle]. These are exactly the same as the periods that were found for luni-solar alignments in paper I, when these alignments were viewed in a frame of reference that was fixed with respect to the Perihelion of the Earth’s orbit.

B. Sub-Decadal Timescales

Paper II showed that if the Perigee-end of the lunar orbit points directly towards (/away from) the Sun on or around:

a) June 21st (i.e. the Summer Solstice), Perigean New (/Full) moons will take place at their furthest points away from the Equator (i.e. at lunar standstills) in the Northern(/Southern) hemisphere.

b) December 21st (i.e. the Winter Solstice), Perigean New (/Full) moons will take place at their furthest points away from the Equator (i.e. at lunar standstills) in the Southern(/Northern) hemisphere.

c) 21st of March or the 21st of September (i.e. the Vernal or Autumnal Equinox, respectively), Perigean New (/Full) moons will take place when these New and Full moons are close to being directly above the Earth’s equator.

Bottom Line: The very process of selecting the times when the Perigean New/Full moons occur at or near seasonal boundaries is in fact equivalent to selecting the times when the strongest Perigean New/Full moon tides either cross the Earth’s equator or when they are at their furthest distance from the Earth’s equator (i.e. lunar standstill).

C. The 31/62-year Perigean New/Full Cycle and El Nino events 

In a series of blog posts in November 2014:

http://astroclimateconnection.blogspot.com/2014/11/evidence-that-strong-el-nino-events-are_13.html

I showed that between 1870 and 2025, the precise alignments between the lunar synodic [phase] cycle and the 31/62 year Perigean New/Full moon cycle, naturally breaks up into six 31-year epochs each of which has a distinctly different tidal property. Note that the second of these 31-year intervals starts with the precise alignment on the 15th of April 1870, with the subsequent epoch boundaries occurring every 31 years after that:

Epoch 1 - Prior to 15th April  1870
Epoch 2 - 15th April 1870 to 18th April 1901
Epoch 3 - 8th April 1901 to 20th April 1932
Epoch 4 - 20th April 1932 to 23rd April 1963
Epoch 5 - 23rd April 1963 to 25th April 1994
Epoch 6 - 25th April 1994 to 27th April 2025

These six tidal epochs naturally break up into two distinct groups depending on whether they start with a New moon or Full Moon.

New Moon Epoch:
Epoch 1 - Prior to 15th April  1870
Epoch 3 - 8th April 1901 to 20th April 1932
Epoch 5 - 23rd April 1963 to 25th April 1994

Full Moon Epochs:
Epoch 2 - 15th April 1870 to 18th April 1901
Epoch 4 - 20th April 1932 to 23rd April 1963
Epoch 6 - 25th April 1994 to 27th April 2025

In addition, I showed that:

Moderate-to-strong El Niño events in the New Moon epochs preferentially occur near times when the lunar line-of-apse aligns with the Sun at the times of the Solstices. Note that this is equivalent to saying that moderate to strong El Niño in New Moon Epochs preferentially occur near times the strongest Perigean New/Full moons are near lunar standstill (e.g. Epoch 5).

Moderate-to-strong El Niño events in the Full Moon epochs preferentially occur near times when the lunar line-of-apse aligns with the Sun at the times of the Equinoxes. Note that this is equivalent to saying that moderate to strong El Niño in Full Moon Epochs preferentially occur near times the strongest Perigean New/Full moons are crossing the Earth's equator (e.g. Epoch 6).

Bottom Line: This means that El Ninos events must be initiated by a physical phenomenon that occurs when the strongest Perigean New/Full moons cross the Earth's equator or when the strongest Perigean New/Full moons reach a lunar standstill. A physical phenomenon that occurs at both the times of lunar crossing and lunar standstill is the tidal forces that lead to a change in sign of the lunar-induced acceleration of the Earth's rotation, roughly once every 7 days.

 D. Lunar Declination and Lunar-Induced Accelerations in the Earth's Rotation.

If you remove the annual and bi-annual seasonal component of the changes in the Earth’s LOD, you are left with the abrupt slowdowns in the Earth's rotation rate (roughly) once every 13.7 days cause by the effects of the lunisolar tides. A more detailed investigation of these semi-monthly changes in Earth’s rotation rate shows that the maxima in LOD (where the Earth is rotating most slowly) occur within a day or so of the time that the Moon crosses the Earth's Equator. This tells you that the slow down in the rotation rate (i.e. the maximum in LOD) is a direct result of the lunar tidal bulge in the Earth's oceans (and atmosphere) being dragged across the Earth's Equator by the Moon. The slow down occurs for much the same reason that a twirling ice-skater slows down their rate of spin by extending their arms i.e. by the conservation of angular momentum.

Similarly, when the lunar tidal bulges in the Earth’s oceans (and atmosphere) reach their furthest point from the Earth’s equator (i.e. highest latitudes where lunar standstills take place), this brings the tidal bulges to their closest point to the Earth’s rotation axis. When this happens, the Earth’s rotation rate increases for the same reason a twirling ice-skater speeds up their rate of spin by pulling in their arms (again by the conservation of angular momentum).

Hence, the bi-monthly variations in LOD are a:

a) maximum (i.e. the slowest rotation rate) near times when the lunar tidal bulges cross the Equator

b) minimum (i.e. the fastest rotation rate) near times when the lunar tidal bulges reach lunar standstill

The following figure shows the connection between the rotation rate of the Earth and the Cardinal locations of the Moon's declination. This figure shows that the maximum rate of change in the Earth's rotation rate take place at (or near) times of lunar standstills (i.e. when the Moon's declination is furthest from the Earth's Equator) and lunar crossing of the Equator [Note the red crosses which mark the times of maximum (lunar-induced) change in the Earth's rotation speed i.e. where the (lunar-induced) acceleration of the Earth's rotation changes sign].  

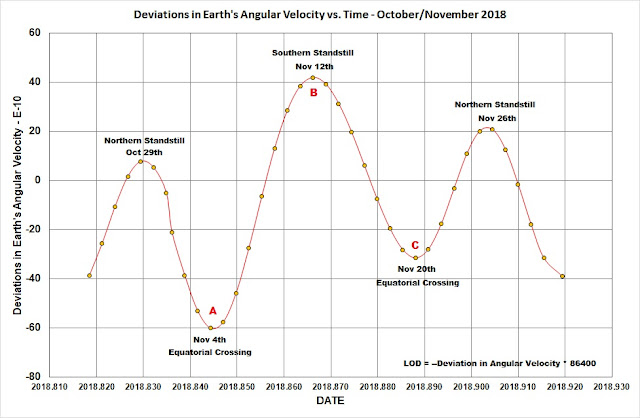
The next figure shows the variation in the Earth's angular velocity (delta omega/omega) between late-October and late-November 2018 [Sidorenkov 2009 - Note that the angular velocity (delta omega/omega) can be converted to LOD in seconds by multiplying by -86400]. Highlighted in this figure are the rough times of the lunar standstills and the lunar crossings of the Earth's Equator. Remember that these correspond to the times where the lunar-induced rotational acceleration of the Earth changes sign. Three points of inflection in the Earth's rotation rate, A, B, and C have been highlighted in the following figure.

SUMMARY

El Ninos are preceded by westerly wind-bursts in the equatorial western Pacific Ocean that decreases the strength of the easterly equatorial trade-winds. These westerly wind-bursts are produced by twin low-pressure cells that straddle the Earth's equator in the western Pacific Ocean. These low-pressure cells are part of the westerly moving equatorial Rossby waves that are generated in near the location of the active phase of a Madden Julian Oscillation (MJO). 

Observational evidence indicates that El Ninos events must be initiated by a physical phenomenon that occurs at times when the Moon is closest to the Earth (i.e. Perigee) and when the lunar-induced acceleration of the Earth's rotation changes sign (i.e. at the times of lunar crossings and lunar standstills).

The lunar-induced acceleration of the Earth changes sign when the lunar-induced atmospheric /oceanic tidal height at the Earth's equator reaches an ebb, either at a tidal minimum (i.e. at a lunar standstill) or at a tidal maximum (i.e. at a lunar equatorial crossing).

This implies that equatorial Rossby waves in the active phase of an MJO are likely to be generated when the lunar-induced atmospheric /oceanic tidal height at the Earth's equator reaches an ebb, either at a tidal minimum (i.e. at a lunar standstill) or at a tidal maximum (i.e. at a lunar equatorial crossing).