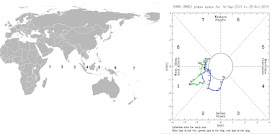
Monday, December 23, 2019
Sunday, December 15, 2019
Will the West Pacific trade winds die down around January 4th 2020?
The following figure shows that the West Pacific trade winds died down around the 17th of September 2019 and two tropical months (i.e. 56.4 days) later around 10th of November 2010.
Ref: https://earth.nullschool.net/#current/wind/surface/level/orthographic=-264.34,3.17,416
Just prior to these two dates, a hybrid combination of an Equatorial Rosby wave and Equatorial Kevin wave, known as a Madden Julian Oscillation (MJO), past just north of Papua New Guinea.
Associated with the Rosby wave component of the MJO were a pair of tropical low-pressure cells located on either side of the Equator that produced a burst of strong westerly winds that dramatically reduced the strength of the West Pacific trade winds a few days later.
The figure below displays the time-longitude plots for 850 hPa westerly wind anomalies covering this period of time. It clearly shows the Aug-Sep and Oct-Nov MJO events that "kill" the West Pacific trade winds around September 17th and November 10th.
If this pattern repeats itself, then we should expect the strength of West Pacific Trade winds to die down around January 4th, 2020. It will be interesting to see if this is enough to tip the Pacific in its EL Nino mode or will it require a couple more of these (lunar-driven) events.
Ref: https://earth.nullschool.net/#current/wind/surface/level/orthographic=-264.34,3.17,416
Just prior to these two dates, a hybrid combination of an Equatorial Rosby wave and Equatorial Kevin wave, known as a Madden Julian Oscillation (MJO), past just north of Papua New Guinea.
Associated with the Rosby wave component of the MJO were a pair of tropical low-pressure cells located on either side of the Equator that produced a burst of strong westerly winds that dramatically reduced the strength of the West Pacific trade winds a few days later.
The figure below displays the time-longitude plots for 850 hPa westerly wind anomalies covering this period of time. It clearly shows the Aug-Sep and Oct-Nov MJO events that "kill" the West Pacific trade winds around September 17th and November 10th.
Thursday, December 12, 2019
The Lunar Alignment Density Index and the Upcoming 2020 El Nino Event
There have been five major El Nino events between 1996 and 2019. These events occurred in the years: 1997-98, 2002-03, 2006-07, 2009-10, and 2015-16.
These events occur when the Equatorial Southern Oscillation Index (Eq. SOI) is > 0.0 for an extended period of time as shown by the red curve in the first of two figures displayed below.
N.B. For a decription of the Eq. SOI go to:
https://www.climate.gov/news-features/blogs/enso/why-are-there-so-many-enso-indexes-instead-just-one
Wilson and Sidorenkov (2020) have developed a preliminary Lunar Alignment Density Index (LADI) that shows that there are increases in the frequency of periods of close alignment (< 0.6 days) between two lunar cycles, that precede each of these major El Nino events. See the areas in dark blue that are highlighted in the following graph.
The exact nature of the LADI cannot be discussed at this point because it is being submitted for publication in the peer-reviewed literature. Suffice it to say, that index incorporates two distinct lunar cycles that we believe are responsible for the generation of Equatorial Rosby and Kelvin waves.
Reference Eq. SOI: https://www.cpc.ncep.noaa.gov/data/indices/reqsoi.for
What the LADI tells us is that if our hypothesis connecting the two lunar cycles with the generation of Equatorial Rossby and Kelvin Waves is correct, then the should be a major El Nino event sometime in the coming year (i.e. 2020).
It is important to note, however, that the prediction of a 2020 El Nino event is subject to the caveat that we are approaching a period where the 11.2-year (solar-driven) cycle in the strength of the (Equatorial) West Pacific trade winds reaches a maximum sometime in 2021-22 (see the graph below). This could tip the Pacific Ocean towards a La Nina event just after the 2020 El Nino event (i.e. possibly by the 2020-21 southern-hemisphere summer.)
ref: http://www.cpc.ncep.noaa.gov/data/indices/wpac850
Sunday, November 17, 2019
Keeping Track of the Latest MJO Event - 16-17/11/2019
The MJO event has finished crossing the whole of the Equatorial Pacific Ocean. This event has killed the equatorial trade winds across the western 55 % of the equatorial Pacific Ocean. It is also starting to warm the SST anomalies off the west coast of Equador to 2.3 C.
A. 1000 hPa Wind Map.
Ref: https://earth.nullschool.net/#current/wind/surface/level/orthographic=-192.95,0.57,416
B. This time the SST Anomalies off the west coasts of Panama, Columbia & Equador have increased to 2.3 to 2.5 C.
It will be interesting to see if this warming continues and spreads south towards the west coast of Peru!
Saturday, November 9, 2019
Keeping Track of the Latest MJO Event - 09/11/2019 15:00 UT
The tradewinds have died over the western half of the Equatorial Pacific Ocean!
Ref: https://earth.nullschool.net/#2019/11/09/1500Z/wind/isobaric/1000hPa/orthographic=-147.51,-0.00,416/loc=-127.538,-57.670
There is one piece of telling evidence that links this phenomenon to the lunar tides.
The following image shows a comparison between the current 1000 hPa wind map [10-11-2019 03:00 UTC - on the right] with the corresponding 1000 hPa wind map almost exactly 2.0 tropical months (= 54.6 days) earlier [17-09-2019 03:00 UTC - on the left] [N.B. This is a difference equivalent to 54.0 days].
In addition (to within 4.0 hours) these images closely correspond to times when the sub-lunar point is crossing the Earth's equator (moving from southwest to northeast along the lunar orbit), as shown in the next image.
There is one piece of telling evidence that links this phenomenon to the lunar tides.
The following image shows a comparison between the current 1000 hPa wind map [10-11-2019 03:00 UTC - on the right] with the corresponding 1000 hPa wind map almost exactly 2.0 tropical months (= 54.6 days) earlier [17-09-2019 03:00 UTC - on the left] [N.B. This is a difference equivalent to 54.0 days].
In addition (to within 4.0 hours) these images closely correspond to times when the sub-lunar point is crossing the Earth's equator (moving from southwest to northeast along the lunar orbit), as shown in the next image.
Coincidence? Not likely!!
Wednesday, November 6, 2019
Keeping Track of the Latest MJO Event - 04/11/2019
The MJO has just started breaking into the Western Pacific Ocean!
It is producing Westerly Wind Bursts (WWBs) just to the north of New Guinea!!
The equatorial trade winds have died wester-ward of 165 E longitude!!!
Let the fireworks begin!!!!
Additional graph added 07/11/2019
A. Location
It is producing Westerly Wind Bursts (WWBs) just to the north of New Guinea!!
The equatorial trade winds have died wester-ward of 165 E longitude!!!
Let the fireworks begin!!!!
Additional graph added 07/11/2019
A. Location
B. 1000 hPa Near-Surface Wind Map - Showing the developing Westerly Wind Bursts (WWBs)
C. 70 hPa Wind Map - Showing an Eq. Kelvin Wave beginning to de-couple from the MJO
D. And people wonder how (many of) the tropical storms in South Asia are generated!
Saturday, November 2, 2019
Red Pill 4 - Take this Red Pill and You Start Seeing Reality!
 |
| You are now are deep down the rabbit hole and you are beginning to see the real world! |
[Please click on the "RED PILL 1, 2 & 3" links if you haven't read these red pills.]
RED PILL 1 The influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric pressure can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycle.
RED PILL 2 If the lunisolar atmospheric tides that are associated with the Peak Seasonal Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 3.8-year (= 1/5th the Metonic Cycle).
RED PILL 3 If the lunisolar atmospheric tides that are associated with the Peak Seasonal Draconic Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 9.3-year (= 1/2th the 18.6-year precession cycle of the lunar line-of-nodes).
RED PILL 4 supports the conclusion that long-term changes in the lunar tides caused by the slow (18.6-year) precession of the tilt of the lunar orbit with respect to the Ecliptic, in combination with the more dominant solar-driven seasonal cycles, play an important role in determining the observed inter-annual to decadal variations of the peak latitude anomaly of the summer (DJF) subtropical high-pressure ridge over Eastern Australia (Lsa) between 1860 and 2010.
THERE ARE FIVE MAIN TAKEAWAYS FROM RED PILL 4
1. This post looks for evidence of a correlation between long-term changes in the lunar tidal forces and the interannual to decadal variability of the peak latitude anomaly of the summer (DJF) subtropical high-pressure ridge over Eastern Australia (Lsa) between 1860 and 2010.
2. A simple "resonance" model is proposed that assumes that if lunar tides play a role in influencing Lsa, it is most likely one where the tidal forces act in "resonance" with the changes caused by the far more dominant solar-driven seasonal cycles. With this type of model, it is not so much in what years do the lunar tides reach their maximum strength, but whether or not there are peaks in the strength of the lunar tides that re-occur at the same time within the annual seasonal cycle.
3. The “resonance” model predicts that if the lunar atmospheric tides associated with the seasonal peak lunar cycles have a measurable effect upon Lsa then there should be significant oscillatory signals in Lsa that vary in-phase with the 9.31-year seasonal peak draconic spring tides, and the 3.80-year seasonal peak spring tides.
4. This is exactly what we see in the real world Lsa data over Eastern Australia between 1860 and 2010. Wilson [6] identifies significant peaks in the spectrum of Lsa at 9.4 (+0.4/-0.3) and 3.78 (± 0.06) tropical years. In addition, the study shows that the observed 9.4-year signal is in-phase with the draconic tidal cycle.
5. Thus, red pill 4 supports the conclusion that long-term changes in the lunar tides caused by the slow (18.6-year) precession of the tilt of the lunar orbit with respect to the Ecliptic, in combination with the more dominant solar-driven seasonal cycles, play an important role in determining the observed inter-annual to decadal variations of the peak latitude anomaly of the summer (DJF) subtropical high-pressure ridge over Eastern Australia (Lsa) between 1860 and 2010.
A. The Sub-Tropical High-Pressure Ridge
1. The Hadley atmospheric circulation cells ensure that the Earth is surrounded by two broad bands of high-pressure roughly located 30 degrees north and south of the Equator. These bands of high pressure are known as the Sub-Tropical High-Pressure Ridge (STHR).
1. The Hadley atmospheric circulation cells ensure that the Earth is surrounded by two broad bands of high-pressure roughly located 30 degrees north and south of the Equator. These bands of high pressure are known as the Sub-Tropical High-Pressure Ridge (STHR).
2. The peaks of the STHRs slowly drift from north to south, and vice versa, with the seasons.
3. During the Southern Hemisphere Winter (in July), the peak of the Southern STHR is located at roughly 27 S.
3. During the Southern Hemisphere Winter (in July), the peak of the Southern STHR is located at roughly 27 S.
4. On average, the centre of the Southern STHR moves south by six degrees to 33 S during the height of the Southern Hemisphere Summer (i.e. January), with the peak of the pressure ridge moving as far as 42 to 43 S during the latter half of summer (i.e. February).
5. During the summer months (DJF), there are four semi-permanent high-pressure cells embedded within the Southern STHR. The first is centered on the island of Tahiti in the South Pacific, the second is centered on the island of Tristan Da Cunha in the South Atlantic, the third is located off the west coast of Australia in the Indian ocean, and the fourth is located off the South-Eastern coast of Australia. The latter is often split between the Tasman Sea and the Great Australian Bight with the relative strength and location of the two cells changing over time.
B. The Peak of the Sub-Tropical High-Pressure Ridge Over Eastern Australia
The UK Met Office Hadley-Centre (UKMO) has published a data set called hadSLP2r.asc (Adam and Ansell [1]; www.hadobs.org [2]) that contains the mean monthly sea-level pressure (MSLP), averaged over 5 x 5-degree latitude-longitude bins, between the years (January) 1850 to (June) 2010.
The hadSLP2r data has been used to create a meridional profile of the MSLP, for each of the summer months (i.e. December, January, and February) for the years 1852 to 2010 (hereafter referred to as the UKMO data set). This has been done by taking a latitudinal average of three 5 x 5-degree bins centered at 140E, 145E, and 150E, for each 5-degree step in latitude between 0 and 65 degrees south. N.B.
the profile data points have not been weighted to correct for
the difference in area between 5 x 5-degree bins with
changing latitude.
The following figure shows the ranges in latitude and longitude over the Australian Continent that are used to create the mean meridional profile for the summer months (DJF), for each year between 1852 and 2010.
The following figure shows a meridional profile of the MSLP for
February 1984.
The profile shown in this figure is a typical example of the meridional profiles found in the UKMO data set. In this profile, we can see a zone of low pressure produced by the Summer Monsoonal Trough centered near 10 degrees S, a ridge of high pressure produced by the STR near 40 deg S, and the second zone of low pressure, south of 60 degrees, that is associated with the Sub-Polar Trough.
Bezier Functions (Microsoft Excel) and Cubic Spine curves were fitted to each of the monthly meridional profile curves to determine their peak latitudes (L). Monthly anomalies for L were obtained using a mean
monthly value of L for the base period 1961-1990 (William
and Stone [3]).
William and Stone [3] point out that it is
important to investigate the monthly anomaly of L on a
seasonally-averaged, rather than annually-averaged basis.
Following their advice, we have taken the latitude anomalies
for December, January, and February for each year and
averaged them together to give a mean summer value for the
anomaly of L (hereafter referred to as Lsa) for all of the
years from 1851 to 2010. N.B. Lsa is defined so that a positive
value means that the STR is north of the mean latitude for
that summer season.
The following figure shows the anomaly of the peak latitude of the Summer Sub-Tropical High-Pressure Ridge over Eastern Australia (Lsa) for the years from 1851 to 2010.
A program called Redfit 3.8e (Schulz and Mudelsee [4])
was used to generate a Lomb-Scargle periodogram of the LSA
data set. The parameters used in the configuration file
needed to run Redfit were set to values that maximize the spectral resolution of the periodogram (N.B. for a detailed
description of the parameters used with Redfit see Schulz
and Mudelsee [4]).
The resulting spectrum is displayed in the figure below. The output of Redfit program indicates that the noise in the periodogram is consistent with an AR1 (red-noise) process.
The solid continuous dark line running across the top of the
spectrum in the figure is the critical false alarm level (CFAL)
(Thomas [5]). Any periodic signals that have peak
amplitudes exceeding this threshold level are believed to be
inconsistent with an AR1 origin and so are considered
significant.
Hence, the only significant peaks in the spectrum
in the following figure are those at 9.4 (+0.4/-0.3) and 3.78 (± 0.06)
(N.B. the errors of the periods given are set at ± half of the
6dB bandwidth). The 9.4-year peak is consistent with the
period of the 9.3-year seasonal draconic spring tidal cycle and the 3.8
year peak with the 3.8 year period of the seasonal spring tidal cycle.
(A Lomb-Scargle periodogram of the LSA data set. The spectral amplitude is scaled such that the area under the spectrum is an estimator for the data variance.)
What this spectrum tells us is that the variations in the latitude anomaly of the peak of the summer (DJF) STHR over Eastern Australia exhibit the same period as that of the 18.6-year draconic tidal cycle (Wilson [6]).
In essence, what this means is that, on average, the latitude of the peak of the STHR moves back and forth in latitude by one degree between the years where the Line-of-Nodes of the lunar orbit points directly towards or away from the Sun at the time of Perihelion, and the years where the Line-of-Nodes is at right angles to the Earth-Sun line at the time of Perihelion.
In essence, what this means is that, on average, the latitude of the peak of the STHR moves back and forth in latitude by one degree between the years where the Line-of-Nodes of the lunar orbit points directly towards or away from the Sun at the time of Perihelion, and the years where the Line-of-Nodes is at right angles to the Earth-Sun line at the time of Perihelion.
References
[1] Allan RJ, Ansell TJ. A new globally complete monthly historical
mean sea level pressure data set (HadSLP2): 1850 – 2004. J
Climate 2006; 19: 5816-42.
[2] www.hadobs.org, hadSLP2r, accessed: Mar 2011.
[3] Williams AJ, Stone RC. An assessment of relationships between
the Australian subtropical ridge, rainfall variability, and high-latitude circulation patterns. Int J Climatol 2009; 29: 691-709.
[4] Schulz M, Mudelsee M. REDFIT: estimating red-noise spectra
directly from unevenly spaced paleoclimatic time series. Comp
Geosci 2002; 28: 421-6.
[5] Thomson DJ. Time series analysis of Holocene climate data.
Philosophical Trans R Soc Lond Ser A 1990; 330: 601-16.
[6] Wilson I.R.G. Lunar tides and the long-term variation of the peak latitude anomaly of the summer Sub-Tropical High-Pressure Ridge over Eastern Australia. Open Atmos Sci J 2012; 6: 49-60.
[6] Wilson I.R.G. Lunar tides and the long-term variation of the peak latitude anomaly of the summer Sub-Tropical High-Pressure Ridge over Eastern Australia. Open Atmos Sci J 2012; 6: 49-60.
The Third Red Pill - Seasonal Peak Draconic Spring Tides
You will have to make an effort if you want to swallow Red Pill 3
[Please click on the "RED PILL 1 & 2" links if you haven't read these red pills.]
RED PILL 1 The influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric pressure can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycle.
RED PILL 2 If the lunisolar atmospheric tides that are associated with the Peak Seasonal Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 3.8-year (= 1/5th the Metonic Cycle).
RED PILL 3 If the lunisolar atmospheric tides that are associated with the Peak Seasonal Draconic Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 9.3-year (= 1/2th the 18.6-year precession cycle of the lunar line-of-nodes).
There are four factors that can affect the strength of seasonal peak tides i.e. peaks in the lunisolar tides that align with the seasons:
1. The proximity of the Earth/Moon system to the Sun.
2. The relative position of the Moon with respect to the Sun i.e. the Moon's phase.
3. The proximity of a New/Full Moon to one of the nodes of the lunar orbit.
4. The proximity of a New/Full Moon to the perigee/apogee of the lunar orbit.
The red-pill 3 blog post will specifically deal with the factor that affects the strength of the Seasonal Peak Draconic Spring Tides i.e. factor 3.
GLOSSARY OF IMPORTANT TERMS
The draconic month = 27.212221 days. The time required for the Moon to move from one of the two nodes of its orbit back to the same node.
The tropical year = 365.2421897 days. The length of the seasonal year.
The Proximity of the New/Full Moon to One of the Nodes of the Lunar Orbit
The Moon moves around the Earth in an elliptical orbit that is inclined to the Earth-Sun plane (i.e. the Ecliptic) by ~ 5.1 degrees. This means that the Moon crosses the ecliptic at two points known as the nodes of the lunar orbit.
Hence, stronger than normal spring tides (known as draconic spring tides) occur whenever a New/Full Moon takes place near one of the nodes of the lunar orbit.
The Moon moves from one node back to the same node once every 27.212221 days. This period of time is called the Draconic lunar month.
It turns out that 13 1/2 draconic months are 2.122791 days longer than one topical year. Hence, if a lunar node aligns with the Sun on a given day of the year, 6.410 years will pass before another lunar node aligns with the Sun on roughly the same day of the year.
This is true because 6.410 years is the number of years it takes for, the 2.122791 days per year slippage between 13 1/2 draconic months and the tropical year, to accumulate to half a draconic month of 13.606110 days.
Unfortunately, when a lunar node realigns with the Sun on roughly the same day of the year, the Moon is no longer at the same lunar phase. In order to have a lunar node realign with the Sun on the same day of the year, and for the Moon to return to the same phase (e.g. New/Full Moon) as well, it would take a period of time set by the beat period between 3.796 and 6.410 years i.e. 9.308 years.
Unfortunately, when a lunar node realigns with the Sun on roughly the same day of the year, the Moon is no longer at the same lunar phase. In order to have a lunar node realign with the Sun on the same day of the year, and for the Moon to return to the same phase (e.g. New/Full Moon) as well, it would take a period of time set by the beat period between 3.796 and 6.410 years i.e. 9.308 years.
This means that if a New Moon takes place when one of the lunar nodes points at the Sun, 9.31 years later, a Full Moon will occur when a lunar node points at the Sun. Thus, the spacing between draconic spring tides is 9.31 years, a period equal to half of the 18.61336-year draconic lunar cycle. The latter is the time required for the lunar line-of-nodes to precess once around the Earth with respect to the stars).
The strongest of the seasonal draconic spring tidal events that occur at the times of total or partial solar and lunar eclipses. Hence, real-life evidence of the 9 or 10-year seasonal draconic spring tidal cycle can be seen in you list all total and partial lunar and solar eclipses that fall on or about a certain date.
The following table lists all the 20th century total and partial lunar and solar eclipses that occur within +/- 6 days of the 21 st of September 00:00 UT.
Year____Day____Time from____Eclipse Type___Duration_____Lunar___Lunar____Spacing
_______________dd:hr:min:sec___________________________________________Last Eclipse
1903___Sep 21___00:04:39:52___Total Solar_____2 m 12 sec____NM________________0 years
1912___Sep 26___05:11:45:_____Partial Lunar_____84 m_______FM___Ascending_____9 years
1913___Sep 15__-05:11:12:_____Total Lunar___232 m / 94 m__FM___Ascending___10 years
1922___Sep 21___00:04:40:31___Total Solar______5 m 59 s_____NM________________9 years
1931___Sep 26___05:19:48:_____Total Lunar____228 m / 84 m___FM___Ascending____9 years
1941___Sep 21___00:04:34:03___Total Solar_____3 m 22 s______NM_______________10 years
1950___Sep 26___05:04:17:_____Total Lunar____210 m / 46 m___FM___Ascending____9 years
1960___Sep 20__-01:01:04:_____Partial Solar_______0 m_______NM_______________10 years
1968___Sep 22___01:11:18:46___Total Solar_______40 sec______NM________________8 years
1978___Sep 16__-04:04:56:_____Total Lunar____208 m / 80 m___FM____Descending__10 years
1987___Sep 23___02:03:12:22__Annular Solar_____3 m 49 s_____NM________________9 years
1996___Sep 27___06:02:54:_____Total Lunar____204 m / 70 m___FM____Descending___9 years
1997___Sep 16__-04:05:13:_____Total Lunar___198 m / 62 m___FM___Descending___10 years
Average Spacing From Last Eclispse__________________________________________9.4 years
This shows that the average spacing between peak seasonal draconic spring tides is 9.4 years, which is close to 9.3 years (= half of the 18.6-year precession cycle of the lunar line-of-nodes).
Hence, if the lunisolar atmospheric tides that are associated with the Peak Seasonal Draconic Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 9.3-year (= 1/2th the 18.6-year precession cycle of the lunar line-of-nodes).
References:
Wilson, I.R.G., Lunar Tides and the Long-Term Variation of the Peak Latitude Anomaly of the Summer Sub-Tropical High-Pressure Ridge over Eastern Australia, The Open Atmospheric Science Journal, 2012, 6, 49-60
http://benthamopen.com/ABSTRACT/TOASCJ-6-49
http://benthamopen.com/ABSTRACT/TOASCJ-6-49
Keeping Track of the Latest MJO Event - 31/10/2019
A. Location
B. 1000 hPa Near-Surface Wind Map
C. 850 hPa Wind Map Showing Possible Eq. Rossby Wave over Cambodia
B. 1000 hPa Near-Surface Wind Map
C. 850 hPa Wind Map Showing Possible Eq. Rossby Wave over Cambodia
Friday, November 1, 2019
The Second Red Pill - Seasonal Peak Spring Tides
Red Pill 2 is large!
But the rewards are great if you manage to get it down!!
[Please click on the "RED PILL 1" link if you haven't read this red pill.]
RED PILL 1 The influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric pressure can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycle.
RED PILL 2 If the lunisolar atmospheric tides that are associated with the Peak Seasonal Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at intervals of 3.8-year (= 1/5th the Metonic Cycle).
There are four factors that can affect the strength of seasonal peak tides i.e. peaks in the lunisolar tides that align with the seasons:
1. The proximity of the Earth/Moon system to the Sun.
2. The relative position of the Moon with respect to the Sun i.e. the Moon's phase.
3. The proximity of a New/Full Moon to one of the nodes of the lunar orbit.
4. The proximity of a New/Full Moon to the perigee/apogee of the lunar orbit.
This large red-pill post will specifically deal with the factors that affect the strength of Seasonal Peak Spring Tides i.e. factors 1 and 2.
GLOSSARY OF IMPORTANT TERMS
The synodic month = 29.5305889 days. The time required for the Moon to go from one New/Full moon to the next New/Full moon.
The tropical year = 365.2421897 days. The length of the seasonal year.
A. The Proximity of the Earth/Moon System to the Sun
Due to the elliptical nature (e = 0.0167) of the Earth's orbit, the distance of the Earth/Moon system from the Sun varies between an aphelion (i.e. furthest distance) of 152.1 million km around July 04th to a perihelion (i.e. closest distance) of 147.1 million km on January 3rd. This means that the strength of lunisolar tidal forces near January 03rd are noticeably enhanced compared to those that are near July 04th. Hence, the effects of any long-term seasonal peak tides upon atmospheric pressure will naturally be enhanced if these peak tides are aligned with the date of perihelion.
B. The Relative Position of the Moon With Respect to the Sun i.e. the Moon's phase
What are Spring Tides?
They are higher than normal tides that occur twice every lunar synodic month (= 29.53 days), whenever the Sun, Earth, and Moon are co-aligned at either New or Full Moon.
It turns out that 12 1/2 synodic months are 3.890171 days longer than one tropical year (N.B. from this point forward, the word “year” will mean one tropical or seasonal year = 365.2421897 days unless indicated).
Hence, if a spring tide occurs on a given day of the year, 3.796 years will pass before another spring tide occurs on roughly the same day of the year.
This is true because 3.796 years is the number of years it takes for, the 3.890171 days per year slippage between 12 1/2 synodic months and the tropical year, to accumulate to half a synodic month of 14.7652944 days.
In the real world, it turns out that Spring Tides occur on roughly the same day of the year once every:
3 years
3 + 4 = 7 years
3 + 4 + 4 = 11 years
3 + 4 + 4 + 4 = 15 years
3 + 4 + 4 + 4 + 4 years = 19 years
[N.B. The 3-year spacing can occur at any point in the 19-year Metonic Cycle sequence]
with the 3:4:4:4:4-year spacing pattern [which has an average spacing of (3 + 4 + 4 + 4 + 4)/5 = 3.8 years], repeating itself after a period of almost exactly 19 years. The 19.0-year period is known as the Metonic cycle. This cycle results from the fact that 235 Synodic months = 6939.688381 days = 19.000238 Tropical years.
Displayed below is a real-life example of one Metonic Cycle between 1996 and 2015.
YEAR____PHASE____DATE____TIME____GAP IN YEARS
1996_____FM_______Sept 27____02:51____ 0 years
1999_____FM_______Sept 25____10:53____ 3 years
2003_____NM_______Sept 26____03:09____ 3 + 4 years = 7 years
2007_____FM_______Sept 26____19:47____ 3 + 4 + 4 years = 11 years
2011_____NM_______Sept 27____11:09____ 3 + 4 + 4 + 4 years = 15 years
2015_____FM_______Sep 28_____02:52____ 3 + 4 + 4 + 4 + 4 years = 19 years
Hence, If the lunisolar atmospheric tides that are associated with the Peak Seasonal Spring Tides play a role in influencing the Earth's atmospheric pressure, you should see variations in this pressure that occur at 3.8-year (= 1/5th the Metonic Cycle) intervals.
References:
Wilson, I.R.G., Lunar Tides and the Long-Term Variation of the Peak Latitude Anomaly of the Summer Sub-Tropical High-Pressure Ridge over Eastern Australia, The Open Atmospheric Science Journal, 2012, 6, 49-60
http://benthamopen.com/ABSTRACT/TOASCJ-6-49
http://benthamopen.com/ABSTRACT/TOASCJ-6-49
Thursday, October 31, 2019
The First Red Pill - How Can You Weaponize the Lunar Atmospheric Tides When it Comes to Climate?
As Morpheus so famously said to Thomas Anderson in the movie "The Matrix":
"This your last chance. After this, there is no turning back. You take the blue pill, the story ends. You wake up in your bed and believe whatever you want to. You take the red pill, you stay in Wonderland, and I show you how deep the rabbit hole goes. Remember, all I'm offering is the truth. Nothing more."
This is the first of series of multiple posts that offers you the opportunity to EITHER, take the blue pill and continue to believe what the Australian Bureau of Meteorology (BOM) tells you about Australia's climate OR take the red pill and open your mind to an alternative reality.
The most significant large-scale systematic variations of the atmospheric pressure, on an inter-annual to decadal time scale, are those caused by the seasons. These variations are predominantly driven by the change in the level of solar insolation with latitude that is produced by the effects of the Earth's obliquity (i.e. the tilt of its rotation axis with respect to the Earth-Sun plane) and its annual motion around the Sun (i.e. its orbit).
This raises an important question: What is the most effective way for cycles in the lunisolar atmospheric tides to influence the Earth's atmospheric pressure, on inter-annual to decadal time scales?
One way is that the lunisolar atmospheric tides can act independently of the variations in atmospheric pressure caused by the seasonal changes in the level of solar insolation with latitude.
If this was true, you would expect to see long-term periodicities in the atmospheric pressure records that would match periodicities of the most extreme peak lunar tides.
An alternative way is that the lunar atmospheric tides could act in "resonance" with (i.e. subordinate to) the atmospheric pressure changes caused by the far more dominant solar-driven seasonal cycles.
With this type of simple “resonance” model, it is not so much in what years do the atmospheric lunar tides reach their maximum strength, but whether or not there are peaks in the strength of the lunar atmospheric tides that re-occur at the same time within the annual seasonal cycle.
"This your last chance. After this, there is no turning back. You take the blue pill, the story ends. You wake up in your bed and believe whatever you want to. You take the red pill, you stay in Wonderland, and I show you how deep the rabbit hole goes. Remember, all I'm offering is the truth. Nothing more."
This is the first of series of multiple posts that offers you the opportunity to EITHER, take the blue pill and continue to believe what the Australian Bureau of Meteorology (BOM) tells you about Australia's climate OR take the red pill and open your mind to an alternative reality.
RED PILL 1 The influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric pressure can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycle.
Q1. How Can You Weaponize the Lunar Atmospheric Tides When it Comes to Climate?
The most significant large-scale systematic variations of the atmospheric pressure, on an inter-annual to decadal time scale, are those caused by the seasons. These variations are predominantly driven by the change in the level of solar insolation with latitude that is produced by the effects of the Earth's obliquity (i.e. the tilt of its rotation axis with respect to the Earth-Sun plane) and its annual motion around the Sun (i.e. its orbit).
This raises an important question: What is the most effective way for cycles in the lunisolar atmospheric tides to influence the Earth's atmospheric pressure, on inter-annual to decadal time scales?
One way is that the lunisolar atmospheric tides can act independently of the variations in atmospheric pressure caused by the seasonal changes in the level of solar insolation with latitude.
If this was true, you would expect to see long-term periodicities in the atmospheric pressure records that would match periodicities of the most extreme peak lunar tides.
An alternative way is that the lunar atmospheric tides could act in "resonance" with (i.e. subordinate to) the atmospheric pressure changes caused by the far more dominant solar-driven seasonal cycles.
With this type of simple “resonance” model, it is not so much in what years do the atmospheric lunar tides reach their maximum strength, but whether or not there are peaks in the strength of the lunar atmospheric tides that re-occur at the same time within the annual seasonal cycle.
So the answer our original question is that, strong peaks in the lunar tidal forces that slowly drift through the seasons, with each advancing year, may not be as effective at influencing the Earth's atmospheric pressure distribution, as weaker tidal peaks that appear at precisely the same time during the seasonal year (hereafter referred to as seasonal peak tides).
In essence, the influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycles.
In essence, the influence of cycles in the atmospheric lunar tides upon the Earth's atmospheric can be re-inforced (i.e weaponized) if they constructively interfere with the annual seasonal cycles.
Sunday, October 27, 2019
Keeping Track of the Latest MJO Event - Update 25/10/2019
A. Location
C. 850 hPa - Wind Map Showing Embedded Equatorial Rossby Wave in MJO
B. 1000 hPa Near-Surface Wind Map
Monday, October 21, 2019
Keeping Track of the Current Madden Julian Oscillation (MJO) Event
19/10/2019 06 UT
A. Location
B. 1000 hPa Near-Surface Wind Map
A. Location
B. 1000 hPa Near-Surface Wind Map
70 hPa - 18km Altitude Wind Map - Showing an embedded Kelvin Wave in the MJO
Tuesday, October 15, 2019
Tuesday, October 8, 2019
A Luni-Solar Connection to Weather and Climate III: Sub-Centennial Time Scales
Wilson, I.R.G. and Sidorenkov, N.S., 2019, A Luni-Solar Connection to Weather and Climate III: Sub-Centennial Time Scales, The General Science Journal, 7927
The following figure shows the raw HadCRUT4 monthly (Land + Sea) world mean temperature anomaly (WMTA) data from 1850 to 2017 (grey line – Climatic Research Unit, University of East Anglia, 2017).https://crudata.uea.ac.uk/cru/data/temperature/
Following the method used by Copeland and Watts (2009), a Hodrick Prescott filter (Hodrick and Prescott 1981 - using λ = 129,0000) is applied to the raw WMTA data to produce a smoothed temperature anomaly curve (Excel Plugin 2019). The resulting smoothed anomaly curve is superimposed upon the raw WMTA data in the figure below (red line).
The Hodrick Prescott filter is designed to separate a time-series data into a trend component and a cyclical component using a technique that is equivalent to a cubic spline smoother. It acts as a low-pass filter that smooths out short-term temperature fluctuations, leaving behind the unattenuated long-term oscillatory signals (Copland and Watts 2009). Given the specific value of λ used here, this effectively translates to a band-pass that eliminates all the oscillatory temperature signals that have periods ≤ 7.0 years (Copland and Watts 2009).
Investigations of climate change generally
involve the study of "forcings" upon the climate system. These are
expressed in power terms that are measured in W m-2. This means that
the best way to study temporal changes in these "forcings" is to look
at time series of the first differences in the total energies that are
associated with each forcing. Similarly, the mean temperature of the Earth's
atmosphere is a measure of its total energy content. Thus, the best way to
study the changes in the climate "forcings" that impact the mean
temperature of the Earth's atmosphere is to look
at time-series of the first difference in world-mean temperature, rather than
time-series of the temperature itself [Goodman 2013].
Following this train of logic, the first
difference curve of the smoothed trend component of the WMTA time series is
calculated in degrees Celsius per month. The resultant first difference curve
(multiplied by an arbitrary factor of 150) is plotted in the figure below (blue
curve). Superimposed upon this is the raw temperature anomaly data (light-grey
curve) and the smoothed trend component (red curve), displayed in units of
degrees Celsius.
The
blue dashed curve in the figure below shows a superposition of a sine wave of
amplitude 1.0 unit and period 9.1 tropical years with a sine wave of amplitude
2.0 units and period 10.1469 (= 9 FMC’s) tropical years. Note that the units
used are degrees Celsius per month times 1000. The actual function used in this figure is:
where
t is the date expressed in decimal Gregorian years [N.B. For the purposes of
this study, this curve will be referred
to as the lunar tidal forcing curve – i.e. LTF curve].
Overlaying this is a red curve which is simply a reproduction of the difference plot of the smoothed
component of the WMTA from the
earlier figure [N.B. For the purposes of this study, this curve will be referred
to as the difference of the smoothed temperature anomaly curve – i.e. DSTA.
It has units measured in degrees Celsius per month. In addition, the DSTA curve
values have been scaled-up by a factor of 1000 to roughly match the variance of
the LTF curve. This is done to aid the comparison between these two curves.
from the
earlier figure [N.B. For the purposes of this study, this curve will be referred
to as the difference of the smoothed temperature anomaly curve – i.e. DSTA.
It has units measured in degrees Celsius per month. In addition, the DSTA curve
values have been scaled-up by a factor of 1000 to roughly match the variance of
the LTF curve. This is done to aid the comparison between these two curves.
A comparison of the DSTA and LTF curves shows
that that the timing of the peaks in the LTF curve closely match those seen in
the DSTA curve for two 45-year periods.
The first going from 1865 to 1910 and
the second from 1955 to 2000. Note that these years are delineated by the black
vertical lines in this figure. During these two epochs, the aligned peaks of the
LTF and the DSTA curves are separated from adjacent peaks by roughly the 9.6
years, which is close to the mean of 9.1 and 10.1469 years. This is in stark
contrast to the 45-year period separating these two epochs (i.e. from 1910 to
1955), and the period after the year 2000, where the close match between the
timing of the peaks in LTF and DSTA curves breaks down, with the DSTA peaks
becoming separated from their neighboring peaks by approximately 20 years.
Hence, the variations in the rate of change of the smoothed HadCRUT4
temperature anomalies closely follow a “forcing” curve that is formed by the
simple sum of two sinusoids, one with a 9.1-year period which matches that of
the lunar tidal cycle, and the other with a period of 10.1469-year
that matches that of half the Perigean New/Full moon cycle. This is precisely
what you would expect if the natural periodicities associated with the Perigean
New/Full moon tidal cycles were driving the observed changes in the world mean
temperature on decadal time scales.
References:
Copeland, B. and
Watts, A., 2009, Evidence
of a Luni-Solar Influence on the Decadal and Bi-decadal Oscillations in
Globally Averaged Temperature Trends, retrieved at:
Lunar-Solar Influence on SST March 1st, 2013,
Greg Goodman
Hodrick, R.
Prescott, E., 1997, Postwar US
business cycles: an empirical investigation.
Journal of Money, Credit, and Banking. 29(1): pp. 1-16. Reprint of
University of Minneapolis discussion paper 451, 1981.